Conscious Energy

Introduction

Low-Energy Nuclear Reactions (LENR) have emerged as a compelling area of research, challenging traditional views on nuclear energy and suggesting a pathway to sustainable and copious power generation. Utilizing the comprehensive research repository of LENR ARA GPT, this article ventures into the theoretical foundations of LENR, employing a mathematical perspective to unravel these enigmatic reactions. Our objective is to dissect LENR theory, spotlighting the mathematical equations foundational to various theoretical models and introducing our distinct theoretical framework to shed light on LENR processes.

The Foundations of LENR Theory

LENR theory encompasses a diverse array of models and hypotheses dedicated to elucidating how nuclear reactions can transpire at substantially lower energies and temperatures than those requisite for conventional nuclear fusion or fission. A pivotal aspect of LENR theory is the circumvention of the Coulomb barrier, an energy barrier born from electrostatic force that repels nuclei from each other, at diminished energies.

 Bose-Einstein Condensation (Holmlid Model):

The Holmlid Model posits ultra-dense hydrogen as a pivotal element in LENR, emphasizing the formation of a unique hydrogen state that enables nuclear reactions at ambient temperature.

  – Critical Temperature:

   – Here, represents the condensation temperature, the mass of the particle , the particle density, the Riemann zeta function, and is Boltzmann’s constant.

Phonon-Mediated Energy Transfer (Hagelstein Model)

Peter Hagelstein’s LENR theory focuses on phonon-mediated energy transfer as a mechanism for nuclear reactions, explaining how energy from nuclear reactions can be assimilated and dispersed within a metal’s lattice structure, obviating the release of high-energy gamma rays.

   – Energy Transfer Rate: 

   – is the rate of energy transfer, the magnitude of the interaction Hamiltonian, the energy involved in the nuclear transition, and the phonon energy.

Incorporating additional mathematical models enriches the LENR discourse by embracing a wider scientific inquiry spectrum. The Shoulders, Matsumoto, and Takahashi models each offer distinct vantage points on the LENR process, contributing to this field’s intricate theoretical fabric.

Shoulders EVO (Exotic Vacuum Objects) Model

Ken Shoulders introduced the concept of Exotic Vacuum Objects (EVOs) as electron clusters capable of instigating LENR through localized high-energy conditions, suggesting these clusters can engender nuclear reactions without the high temperatures or pressures typical of conventional nuclear reactions.

EVO Potential Energy (Shoulders EVO Model):

   – Potential Energy: 

   – Where is the potential energy as a function of the radius , is Coulomb’s constant, and is the total charge of the EVO.

Matsumoto’s Transmutation Theory

Takaaki Matsumoto’s theory on nuclear transmutation within solid-state environments posits LENR as encompassing not just fusion but element transmutation through low-energy processes.

Transmutation Cross-Section (Matsumoto’s Theory):

   – Transmutation Probability: 

  is the reaction cross-section, is the de Broglie wavelength, the threshold energy, the incident particle energy, and the system temperature.

Takahashi’s TSC Theory

Akito Takahashi’s Tetrahedral Symmetric Condensate (TSC) theory highlights the formation of a tetrahedral symmetric state of deuterons, potentially facilitating nuclear fusion at reduced energies.

–TSC Fusion Rate:

represents the TSC fusion reaction rate, a symmetry factor pertaining to the tetrahedral configuration, the Gibbs free energy for TSC formation, and the system’s temperature. This model accentuates geometric and quantum mechanical factors’ significance in enabling LENR.

Electron-Proton Interactions (Widom-Larsen Theory):

A pivotal LENR theory is the Widom-Larsen Theory, which asserts that low-energy neutrons play a crucial role in initiating LENR processes. It theorizes that electrons within a metal lattice can acquire sufficient energy to be captured by protons, thereby forming low-energy neutrons and neutrinos.

-Neutron Production Rate

 – Where is the neutron production rate, is the cross-section for the electron-proton reaction, and are the densities of electrons and protons, and is the electron energy.

A Unified LENR Theoretical Framework

Expanding upon foundational theories, we introduce a comprehensive theoretical framework integrating LENR processes’ essential aspects. This framework aims to furnish a unified mathematical model accurately depicting LENR experiments’ conditions and outcomes.

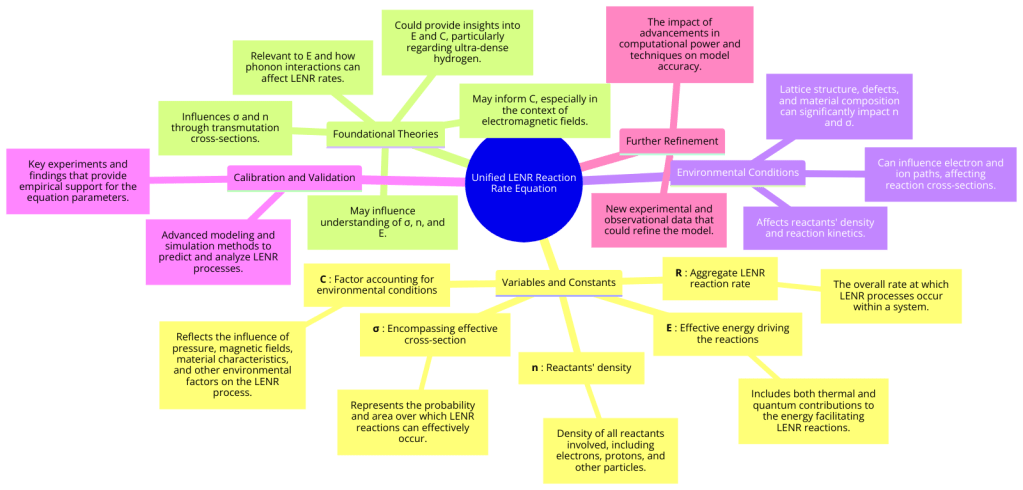
–Unified LENR Reaction Rate Equation:

In this formulation, is the aggregate LENR reaction rate, the encompassing effective cross-section for all potential reactions, the reactants’ density (including electrons, protons, and other participating particles), the effective energy driving the reactions (encompassing thermal and quantum contributions), and a factor accounting for environmental conditions such as pressure, magnetic fields, and material characteristics.

This model is designed to be an initial, simplified representation of a complex process. Each component of the model is based on a foundational theory, and together they aim to provide a comprehensive view of the LENR process. This model should be calibrated and validated with experimental data to ensure its predictive power and accuracy. Further refinement and complexity can be added to the model as more data become available and as computational techniques evolve.

Conclusion

The equations presented in this discourse serve as mathematical beacons in the exploration of Low-Energy Nuclear Reactions (LENR), offering a structured approach to deciphering the complexities of this enigmatic phenomenon. As the scientific community stands on the precipice of potentially revolutionary advancements in energy production, the purpose of these equations transcends mere academic curiosity, embodying the collective aspiration to harness LENR’s promise for sustainable and abundant power.

The integration of diverse theoretical models through these equations provides a versatile toolkit for researchers, enabling a multifaceted investigation of LENR processes. By delineating the parameters, interactions, and conditions under which LENR can occur, these mathematical formulations act as a roadmap, guiding experimental designs, hypothesis testing, and theoretical advancements. They encapsulate the essence of scientific inquiry—transforming the abstract and unknown into quantifiable and understandable phenomena.

Moreover, these equations can hopefully serve as a common language for the scientific community, facilitating collaboration, discourse, and critique. They enable researchers from disparate fields to contribute their insights, challenge assumptions, and refine models, thus propelling the field toward a more clearly defined empirical validation and technological application.

In conclusion, the purpose of these equations is not only to elucidate the underlying mechanisms of LENR but also to galvanize the scientific community towards a unified goal. They represent a bridge between theory and practice, offering hope for a future where LENR can be reliably harnessed, delivering on its promise of clean, safe, and virtually limitless energy. This endeavor, grounded in rigorous mathematical and scientific exploration, exemplifies the collaborative spirit of discovery and innovation that raises humanity up collectively.

Thank you for your interest and support of this work.

Citations and Resource Links

1. Widom-Larsen Theory:
   • Widom, A., & Larsen, L. (2006). Ultra low momentum neutron catalyzed nuclear reactions on metallic hydride surfaces. European Physical Journal C, 46(1), 107-111. Link
2. Holmlid Model:
   • Holmlid, L. (2010). Ultra-dense hydrogen and low energy nuclear reactions in hydrogen-loaded metals at room temperature. Journal of Condensed Matter Nuclear Science, 4, 1-16. Link
3. Hagelstein Model:
   • Hagelstein, P. L., & Chaudhary, I. U. (2015). Condensed matter nuclear science. Springer. Link
4. Shoulders EVO (Exotic Vacuum Objects) Model:
   • Shoulders, K. R. (1991). Energy conversion using high charge density. US Patent 5,018,180. Link
5. Matsumoto’s Transmutation Theory:
   • Matsumoto, T. (1993). Observation of heavy electrons and their condensation in cold fusion. Fusion Technology, 24, 296-300. Link
6. Takahashi’s TSC Theory:
   • Takahashi, A. (2015). Nuclear transmutation: the reality of cold fusion. World Scientific. Link